万物之始,大道至简,衍化至繁
在缠论里级别的问题是很重要的,在原文里也是反复强调,很多新手遇到级别的问题也比较晕,看着看着就糊涂了,网上很多人也花很多心思谢了很多文章来解释级别,我总觉得看了之后更晕了。
我也来解释一下,力争从最简单的角度来解释,争取让人一遍就能看懂。
级别分两种:
1、K线图级别
2、自同构性结构生长出来的级别
下面逐一来分析。
一、K线图级别
这个不用多说,就是K线图时间周期的级别,一般是大家都在用的,1F,5F,30F,日线,周线,月线,直接在软件就能选取。
二、自同构性结构生长出来的级别
这个一般实际应用的少,注重理解,理解了这个概念,很多内容也就容易理解了。
首先,什么是自同构性结构?
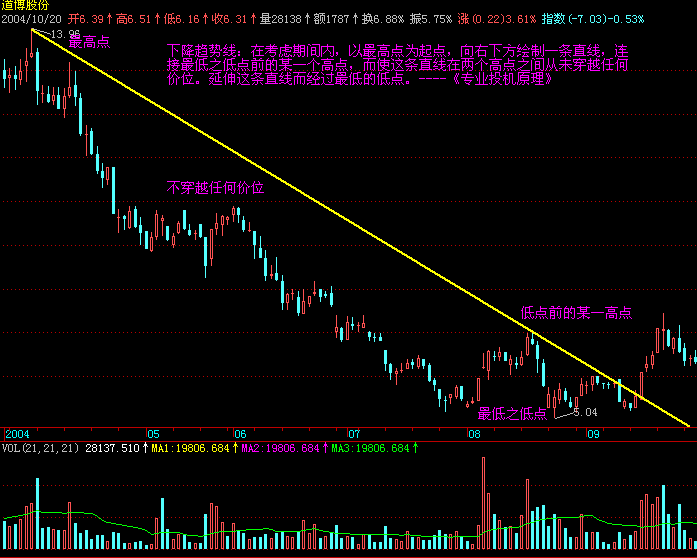
原文中的解释:自同构性结构是走势的最基本结构,在不同级别上(从最低级别到最高级别),其表现的几何形态是相同的。
缠论讲到的分型、走势类型,本质就是自同构性结构。同样,走势必完美的本质也是自同构性结构。例如分型,在1分钟级别是这样的结构,在年线上也是这样的结构。
自同构性结构的自组性:自同构性结构依据时序性、连续性,就可以自组出级别来。自同构性结构的自组性符合原始递归定义,可用递归函数计算出级别。这种自组性决定了这种结构的分解和组合符合结合律,并存在包含关系。
级别,只是按一定的规则,自生长出来的一种分类方法。
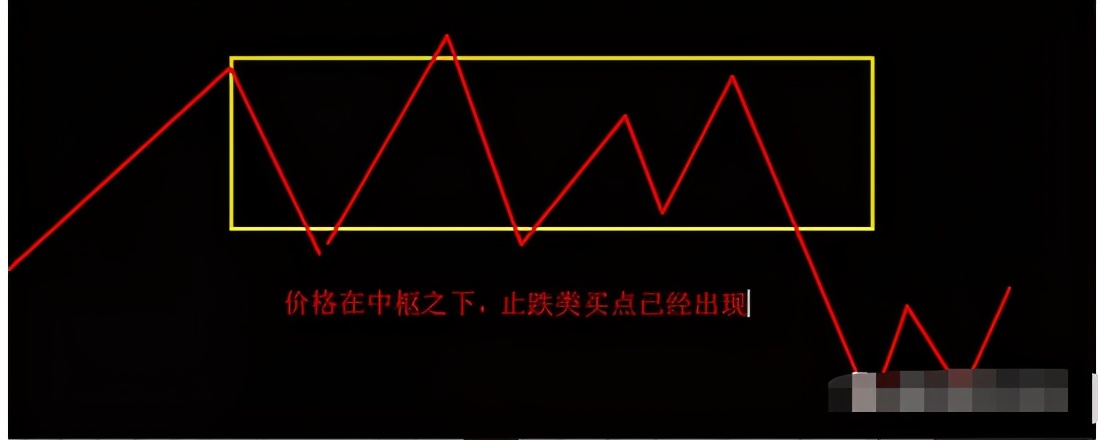
我用一张图,来解释一下级别是怎么生长出来的,其实就是递归的概念。
展开全文
看图来分析一下。
我们以线段为例,青色线段为1F线段,我们把1F线段级别作为最小级别,来往高级别递归。
根据类似线段划分的方法,就能依次递归出高级别的线段,比如说青色的线段,三个线段重叠,形成高级别线段,即图中红色的线段,这里要注意,这个红色的线段,并不能说一定是5F的,可以是任何时间周期的。
同理,红色的可以继续生长出蓝色的线段,蓝色的线段再生长出粉色的线段。
禅师说级别本质上与时间周期无关,其实就是说,从小级别递归出来的高级别,是不能用时间周期来判断的,也无法判断,严格的说,不能按照时间周期来划分。
比如说,1F级别线段,递归出的高一级线段,就一定是5F级别的吗?就一定能在5F图上画出线段来吗?为什么就不能在4F图上或者6F图或其他时间周期上画出线段来呢,当然这只是举例,这个大家仔细理解一下。
之所以应用时间周期来划分级别,禅师也说过,时间只是对级别 分类的一种划分手段,比较符合看软件K线图的习惯,就是为了简便,一笔至少为5根K线,1F图上的1笔就是5F图上的1根K线,所以才有了1F,5F,30F等,都在软件上直接有,应用起来比较顺手,差也不会差太多,如果从最低级别递归上来,看着就太杂乱,而且也没必要。
在实际操作过程中,并不用理解的多么透彻,直接按照时间周期来操作,能分清本级别,次级别,高级别,就足够应付大多数情况了。大道至简。
这种解释不知道能不能看的懂。不知道表达是否到位,望指正。


网友评论
最新评论
是怎么生长出来的,其实就是递归的概念。 展开全文看图来分析一下。我们以线段为例,青色线段为1F线段,我们把1F线段级别作为最小级别,来往高级别递归。根据类似线段划分的方法,就能依次
至少为5根K线,1F图上的1笔就是5F图上的1根K线,所以才有了1F,5F,30F等,都在软件上直接有,应用起来比较顺手,差也不会差太多,如果从最低级别递归上来,看着就太杂乱,而且也没必要。在实际操作过程中,并不用理解的多么透彻,直接按照时间周期来操作,能分清本级别,次级别,高级别,就足够应
中的解释:自同构性结构是走势的最基本结构,在不同级别上(从最低级别到最高级别),其表现的几何形态是相同的。缠论讲到的分型、走势类型,本质就是自同构性结构。同样,走势必完美的本质也是自同构性结构。例如分